Ondas y Sonido Clase 1

Características de una onda

Una onda corresponde a una perturbación de un medio: Es la transmisión de una energía aplicada con frecuencia. Podemos describir los trenes de ondas por medio de dos características:

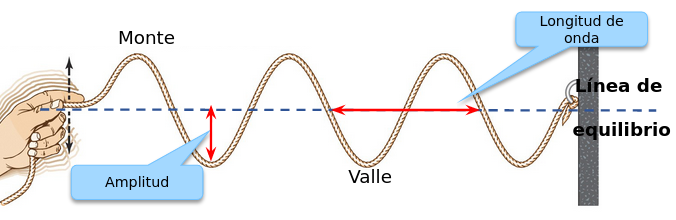
Amplitud

Se refiere a la máxima separación de la onda desde su punto medio. En la onda de sonido, corresponde a lo que llamamos volumen.

Longitud de onda

Es la distancia que recorre un ciclo completo.

Longitud de onda

Podemos estudiar la longitud de onda conociendo la distancia que recorre una onda y su número de ciclos (también llamados oscilaciones). Su unidad de medida en el Sistema Internacional es el metro [m], y se puede medir en cualquier unidad de longitud que corresponda (pie, angstrom, micrón o micrómetro, kilómetro, etc).

En el siguiente ejemplo, consideremos que la onda recorre una distancia de 6 [m]

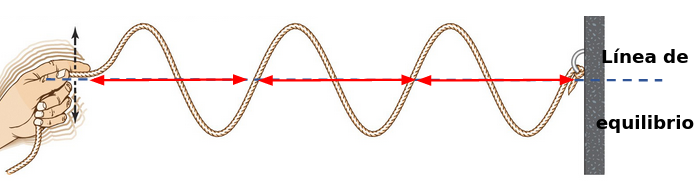
Se puede apreciar que realiza 3 oscilaciones (marcadas con flechas rojas en la imagen) en esos 6 metros. La longitud de onda se puede obtener a partir de esta expresión:

\[\lambda = \frac{distancia}{oscilaciones} \]

Reemplazamos los valores que corresponde: 6[m] es la distancia, y 3 oscilaciones se realizaron.

\[\lambda = \frac{6[m]}{3} \] \[\lambda = 2[m] \]

Frecuencia

Corresponde al número de oscilaciones o ciclos que realiza una partícula por unidad de tiempo. También corresponde al número de pulsos u ondas de un tren de ondas que pasan por un punto en determinado tiempo. Su unidad de medida en el Sistema internacional es el Hertz [Hz] y se calcula como:

\[f = \frac{oscilaciones}{tiempo} \]

Realicemos el cálculo mediante un ejemplo: Considere que la siguiente onda completa su viaje en 9 segundos.

Reemplazamos los 9 segundos y las 3 oscilaciones en la ecuación:

\[f = \frac{3}{9[s]} \] \[f = \frac{1}{3} [Hz]\]

Periodo

Corresponde al tiempo que tarda una partícula en completar un ciclo u oscilación. También corresponde al tiempo que tarda un pulso o una onda en pasar por un punto. Su unidad de medida en el Sistema Internacional de unidades es el segundo, se calcula como:

\[T = \frac{tiempo}{oscilaciones} \]

Consideremos el mismo caso anterior, en que esta onda se demora 9 segundos en completarse:

Reemplazando los valores en la ecuación correspondiente (9 segundos y 3 oscilaciones), tenemos:

\[T = \frac{9[s]}{3} \] \[T = 3[s] \]

Relación entre frecuencia y periodo

Los conceptos de periodo y frecuencia están muy relacionados.

Imagina que esperas un bus…

Probablemente te gustaría saber cuánto tiempo tardará en pasar el siguiente. Al hablar de tiempo en un proceso periódico, estamos usando el concepto de periodo.

En cambio, si quieres saber la cantidad de buses que pasaran en un intervalo de tiempo, por ejemplo, una hora, entonces estas utilizando el concepto de frecuencia.

Si aumentamos el número de buses por hora (frecuencia), entonces disminuimos el tiempo de espera (periodo). En conclusión, periodo y frecuencia son los inversos el uno del otro, lo que se puede expresar matemáticamente así:

\[f = \frac{1}{T} \Longleftrightarrow T = \frac{1}{f} \]

Rapidez

Es la distancia de la onda por unidad de tiempo. Sus unidades en el Sistema Internacional son [m/s] Se calcula como:

\[\nu = \frac{distancia}{tiempo} \]

Como podemos conocer la frecuencia y la longitud de onda, podemos determinar la rapidez de la onda de la siguiente manera:

\[\nu = \lambda \cdot f \]

Continuemos con el ejemplo anterior, donde esta onda se completó en 6[m] y 9 [s], por lo que tiene una \(\lambda\) de 2[m] una frecuencia de \(\frac{1}{3}[Hz] \).

Reemplazando en la ecuación tenemos:

\[\nu = 2[m] \cdot \frac{1}{3}[Hz] \] \[\nu = \frac{2}{3}[m/s] \]