Clase Semana 1: Almacenamiento y transmisión de información mediante algoritmos

Historia de la computación

La máquina analítica de Charles Babbage

Descrita en 1837, mediante sus componentes mecánicos debería poder servir como calculadora general (antes modeló una máquina para calcular tablas de logaritmos). Podría almacenar 1000 números de 50 dígitos cada uno, en base 10 (aproximadamente 16,2 kB).

Esta máquina se modeló a partir de los telares mecánicos y funcionaría a base de vapor. Tristemente los primeros modelos funcionales recién se produjeron 150 años después de su instrucción.

La primera programadora

Augusta Ada King, condesa de Lovelace. Se interesa por la máquina analítica de Babbage y, con su entusiasmo por las matemáticas, diseña un conjunto de instrucciones en tarjetas perforadas para determinar los números de Bernoulli.

Y no solo esto, también Ada visualiza la capacidad de esta máquina programable para relacionar estos números almacenados y sus conversiones con música e incluso imágenes.

De esta manera es también la primera ingeniera en computación.

Cálculo Lambda

En la década del 30, Alonzo Church y Stephen Kleene establecen un sistema formal que permite definir el concepto de función matemática, su aplicación y la recursión.

Las funciones en cálculo lambda son anónimas, además de no poseer estado. Sólo transforman sus entradas en salidas.

\[\lambda_{x,y} \rightarrow x + y\]

Church y Kleene logran demostrar que cualquier cálculo (computación) se puede realizar con las definiciones recursivas del cálculo lambda.

Máquina de Turing

Al igual que su profesor, Alan Turing realiza un aporte a la práctica de las máquinas computacionales:

• Una máquina teórica que puede leer y escribir en una cinta sin fin.
• El problema de la parada.

La máquina de Turing, como se conoce a este modelo, trabajaría en una cinta desde la cual se pueden leer instrucciones, moverse, y finalmente escribir en la cinta, de acuerdo a algún código.

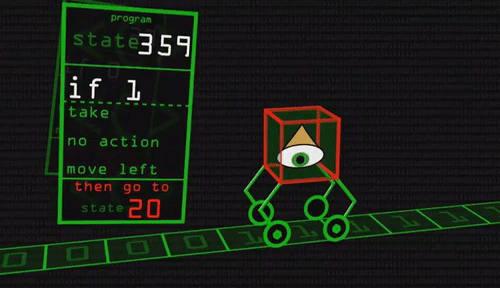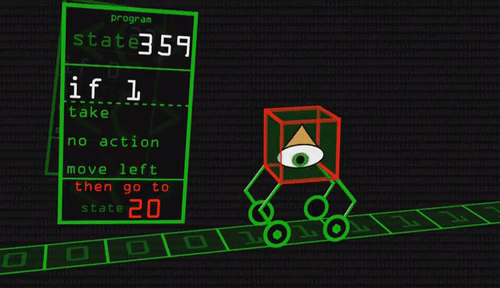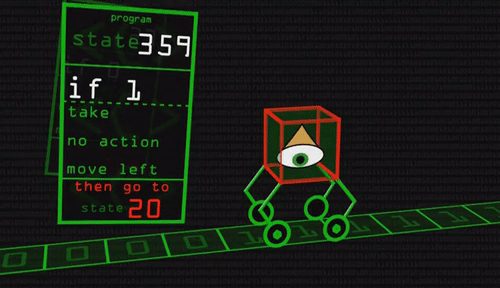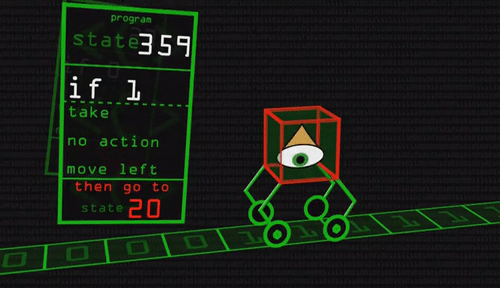
El problema de la parada es algo más complejo: Si se tiene una máquina M, y se le da una instrucción I, ¿Podemos determinar si la máquina procesará I en un número finito de pasos?.

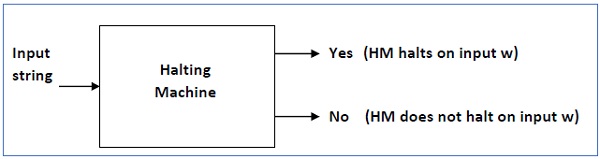
Hipótesis de Church-Turing

Gracias a estos aportes, se pudo obtener dos grandes avances:

• Una máquina que era capaz de modificarse siguiendo un conjunto de instrucciones.
• Un lenguaje formal en el que expresar estas instrucciones.

El cálculo lambda y la máquina de Turing son equivalentes.

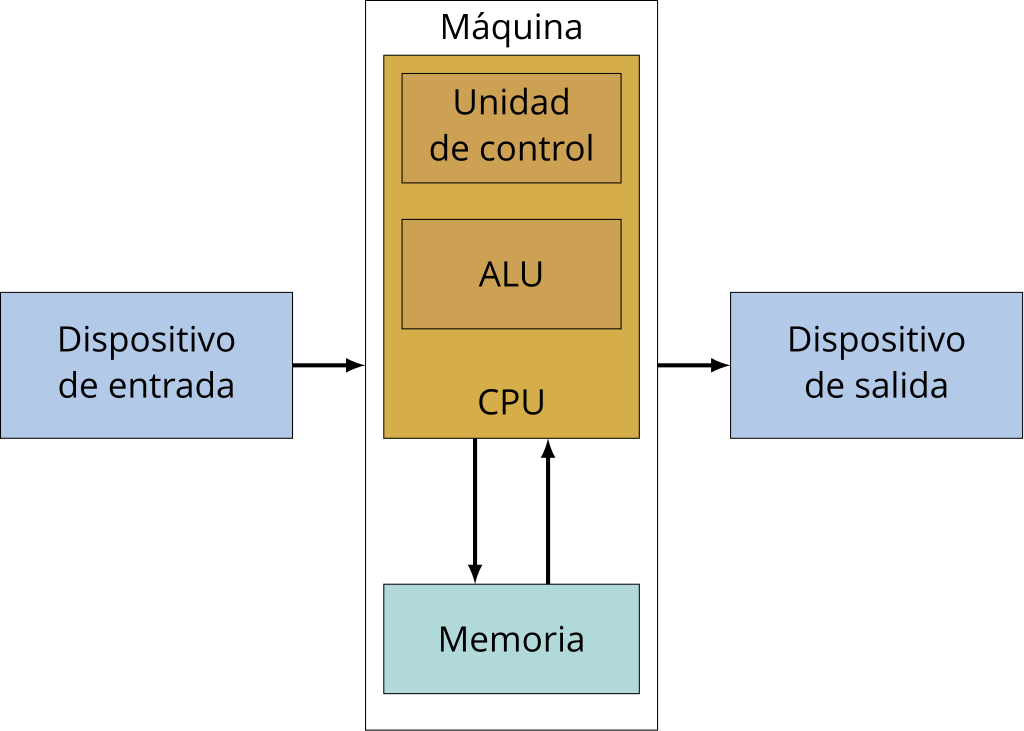
Modelo de Von Neumann

El equipo de físicos a cargo de Jon Von Neumann, describe una arquitectura que permitiría emular (con limitaciones físicas) una máquina de Turing.

Conceptos matemáticos

Algoritmos

Habíamos propuesto que la algorítmica es dar instrucciones por medio de patrones, por ejemplo para calcular la suma de todos los enteros desde el cero:

\[\sum_{i=0}^{i=n} n = (n+1) \cdot \frac{n}{2} \]

¿Cómo se podría representar esto en un lenguaje de programación?

Introducción a LISP

Corresponde a un lenguaje de programación desarrollado por John McCarthy en 1958, por lo que es el segundo lenguaje de programación de alto nivel más antiguo del mundo.

LISP significa LISt Processor (Procesador de Listas), ya que lo que hace es tomar sus unidades atómicas e ingresarlas entre medio de paréntesis.

(list 'A 'B 'C)
'(A B C)

(A B C)
(A B C)

¿Qué son las listas?

• (esto es una lista)
• esto no

Formas especiales en LISP

Cuando una lista tiene como primer elemento una función, el resto de los elementos son sus argumentos y serán evaluados.

• (+ 1 2)
• (* 4 5)
• (expt 2 4)

Definir entidades en LISP

Uno puede definir tanto variables como funciones. En ambos casos, se utiliza la función del lenguaje (define).

(require 2htdp/image)

(define LADO 400)

(define ANCHO 200)

(rectangle LADO ANCHO "solid" "blue")

(object:image% ... ...)

(define (cuadrado-de-x x)
        (* x x))

(cuadrado-de-x 5)

25

Laboratorio de computación

El desafío es animar el aterrizaje de un dibujo de nave espacial, para ello piensa en las siguientes preguntas:

• ¿Qué tipo de datos se necesitan?
• ¿Qué funciones debería definir?
• ¿Cuáles son las entradas y las salidas de esas funciones?
• ¿Tiene Racket algunas bibliotecas con funciones que me ayuden a animar?